技術資料 減速機 小形ギヤモータ 取扱
ここでは、ギヤモートル、ハイポイドモートル、クローゼモータに関する一般取扱について記載しています。
詳細につきましては、製品に添付しています取扱説明書をご参照ください。
トルクアームの設計
標準トルクアームを用いたり、お客様でトルクアームを設計・製作される場合には、次の要領で各要素の強度を確認してください。
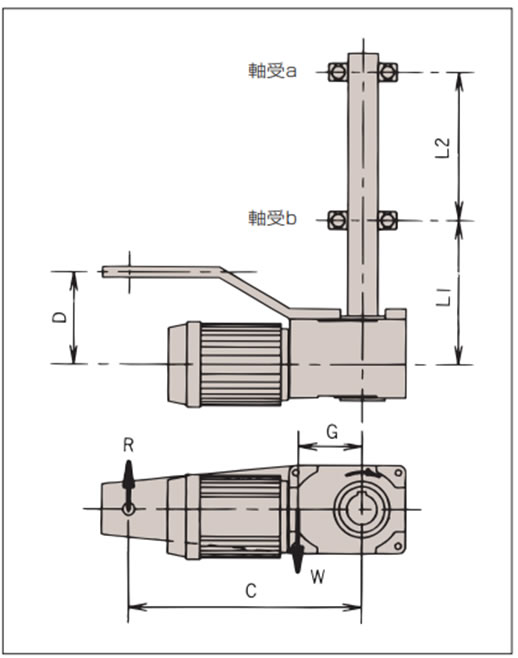
1. トルクアームおよび固定ボルトのチェック
トルクアーム反力Rにより確認してください。
R = T + W × G C
2. 軸受の選定
軸受反力A、Bにより確認してください。
A(軸受a) = L1 × (R - W) - D × R L2
B(軸受b) = (L1 + L2) × (R - W) - D × R L2
- T:出力トルク N・m{kgf・m}
- W:減速機の自重 kg{kgf}
- R:トルクアーム反力 kg{kgf}
- G:被動軸中心と減速機重心間距離 m
- C:被動軸中心と回り止め間の距離 m
- D:減速機中心と回り止め間の距離 m
- L1:減速機中心と軸受b間の距離 m
- L2:軸受aと軸受b間の距離 m
*出力トルクは左図回転方向時+、反対方向時は-となります。
オプショントルクアーム使用時の各寸法(概略値)
| 機種形番 | G |
|---|---|
| HMTA010-30H5~35H1200 HMTA020-30H5~200 HMTA020-45H600~1200 HMTA040-55H600~1200 |
0.10m |
| HMTA020-35H300~480 HMTA040-30H5~35H200 HMTR221-45H5~55H120 |
0.12m |
| HMTR075-35H5~55H480 HMTR151-55H100~200 |
0.13m |
| HMTA040-45H300~480 HMTR151-45H5~80 HMTR370-55H5~60FI |
0.15m |
| HMTR550-55H5~40FI | 0.26m |